Trong toán học, việc tìm tập xác định của một hàm số là bước quan trọng đầu tiên khi nghiên cứu về hàm số đó. Hôm nay, Chia Sẻ Kiến Thức Du Học Canada sẽ hướng dẫn các bạn cách tìm tập xác định của hàm số y = 1/sinx một cách chi tiết và dễ hiểu nhất.
Kiến Thức Cơ Bản Cần Thiết
Khái Niệm Về Tập Xác Định
Tập xác định của một hàm số là tập hợp tất cả các giá trị của biến độc lập x mà tại đó hàm số có giá trị xác định (có nghĩa). Đối với hàm số y = 1/sinx, ta cần đặc biệt lưu ý:
- Đây là một phân thức
- Mẫu số của phân thức là hàm sin x
- Một phân thức chỉ xác định khi mẫu số khác 0

Tính Chất Của Hàm Số Sin x
- Chu kỳ:
- Hàm sin x có chu kỳ 2π
- Giá trị của sin x lặp lại sau mỗi 2π
- Giá trị:
- -1 ≤ sin x ≤ 1
- sin x = 0 tại x = kπ (k ∈ Z)
Phương Pháp Tìm Tập Xác Định
Bước 1: Xét Điều Kiện Mẫu Số Khác 0
Điều Kiện Cần Tránh
- sin x ≠ 0
- x ≠ kπ (k ∈ Z)
Biểu Diễn Toán Học
x ∈ R \ {kπ | k ∈ Z}
Bước 2: Biểu Diễn Tập Xác Định
- Dạng khoảng:
- (-π, 0)
- (0, π)
- (π, 2π)
- Và tiếp tục với các khoảng tương tự
- Dạng tổng hợp: D = R \ {kπ | k ∈ Z}
Phân Tích Chi Tiết
Giải Thích Từng Bước
- Phân tích hàm số:
- Hàm số có dạng phân thức y = 1/sin x
- Mẫu số là hàm sin x
- Tử số là hằng số 1
- Xét điều kiện:
- Mẫu số phải khác 0
- sin x ≠ 0
- x ≠ kπ (k là số nguyên)
Ví Dụ Minh Họa
Ví dụ 1: Xét giá trị x = π/2
- sin(π/2) = 1
- 1/sin(π/2) = 1
- Giá trị này thuộc tập xác định
Ví dụ 2: Xét giá trị x = π
- sin(π) = 0
- 1/sin(π) không xác định
- Giá trị này không thuộc tập xác định

Các Trường Hợp Đặc Biệt
Các Điểm Đặc Biệt
- Các điểm không xác định:
- x = 0
- x = π
- x = -π
- x = 2π
- Các điểm có giá trị tuyệt đối lớn nhất:
- x = π/2 + kπ
- x = -π/2 + kπ
Xem thêm Hướng Dẫn Chi Tiết về Đạo Hàm Logarit Tự Nhiên (ln) Cho Du Học Sinh Canada
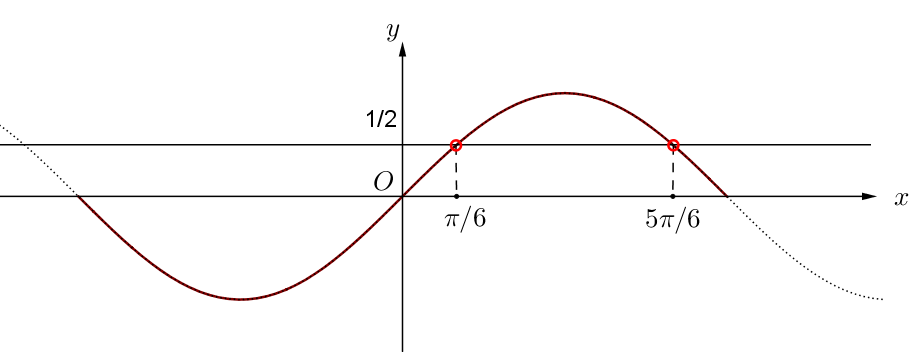
Ý Nghĩa Hình Học
- Đồ thị hàm số:
- Có các tiệm cận đứng tại x = kπ
- Đối xứng qua các điểm (kπ, 0)
- Có dạng hyperbol
- Tính đối xứng:
- Hàm số không có tính đối xứng
- Đồ thị có tính tuần hoàn

Ứng Dụng Trong Thực Tế
Trong Vật Lý
- Dao động điều hòa:
- Tính toán vận tốc
- Tính gia tốc
- Phân tích chuyển động
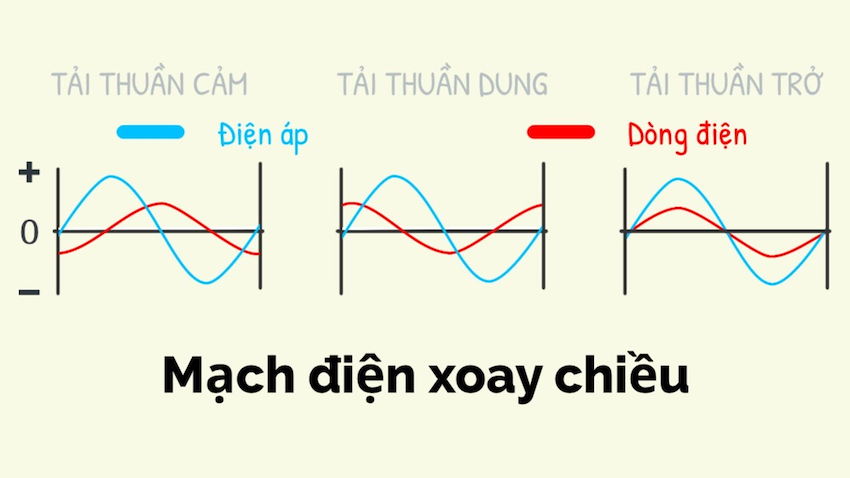
- Điện học:
- Mạch điện xoay chiều
- Tính công suất
- Phân tích tín hiệu
Xem thêm Hướng Dẫn Chi Tiết Công Thức Tính Diện Tích Toàn Phần Cho Du Học Sinh Canada
Trong Kỹ Thuật
- Xử lý tín hiệu:
- Phân tích Fourier
- Lọc tín hiệu
- Điều chế tín hiệu
- Thiết kế:
- Tính toán kết cấu
- Thiết kế mạch điện
- Phân tích rung động
Phương Pháp Ghi Nhớ
Kỹ Thuật Ghi Nhớ
- Quy tắc cơ bản:
- Nhớ các điểm không xác định
- Hiểu tính chu kỳ của hàm
- Nắm vững tính chất đối xứng
- Mẹo thực hành:
- Vẽ đồ thị
- Làm nhiều bài tập
- Liên hệ thực tế
Các Lỗi Thường Gặp
- Lỗi về khái niệm:
- Quên xét mẫu số
- Nhầm lẫn chu kỳ
- Bỏ sót điểm đặc biệt
- Lỗi về kỹ thuật:
- Sai đơn vị đo góc
- Nhầm dấu trong khoảng
- Viết sai biểu thức
Kết Luận và Lời Khuyên
Việc tìm tập xác định của hàm số y = 1/sinx đòi hỏi sự hiểu biết sâu sắc về hàm số lượng giác và các tính chất của nó. Thông qua bài viết này, chúng tôi hy vọng các bạn đã nắm được phương pháp cơ bản và có thể áp dụng vào các bài toán tương tự.
Để được tư vấn thêm về các vấn đề học tập và du học Canada, vui lòng liên hệ:
- Email: [email protected]
- Website: https://canada.net.vn
Đội ngũ giáo viên giàu kinh nghiệm của chúng tôi sẽ giúp bạn giải đáp mọi thắc mắc và hỗ trợ bạn trong quá trình học tập.
