Khi chuẩn bị cho hành trình du học Canada, việc nắm vững kiến thức hình học cơ bản, đặc biệt là cách chứng minh hai tam giác bằng nhau, là vô cùng quan trọng. Hôm nay, canada.net.vn sẽ chia sẻ một bài viết chi tiết về chủ đề này, giúp các bạn học sinh có nền tảng vững chắc cho việc học tập tại Canada.
Tổng quan về tam giác và sự bằng nhau
Định nghĩa cơ bản
Hai tam giác được gọi là bằng nhau khi:
- Có thể chập khít lên nhau
- Các cạnh và góc tương ứng bằng nhau
- Có diện tích bằng nhau
Tầm quan trọng trong hình học
- Nền tảng cho các bài toán phức tạp
- Phát triển tư duy logic
- Ứng dụng trong thực tế
- Cơ sở cho hình học không gian
Các tiêu chuẩn chứng minh hai tam giác bằng nhau
Tiêu chuẩn cạnh – cạnh – cạnh (SSS)
- Ba cạnh của tam giác này bằng ba cạnh của tam giác kia
- Điều kiện áp dụng
- Các bước chứng minh
- Ví dụ minh họa
Xem thêm Cách Tìm Tập Xác Định Của Hàm Số y = 1/sinx
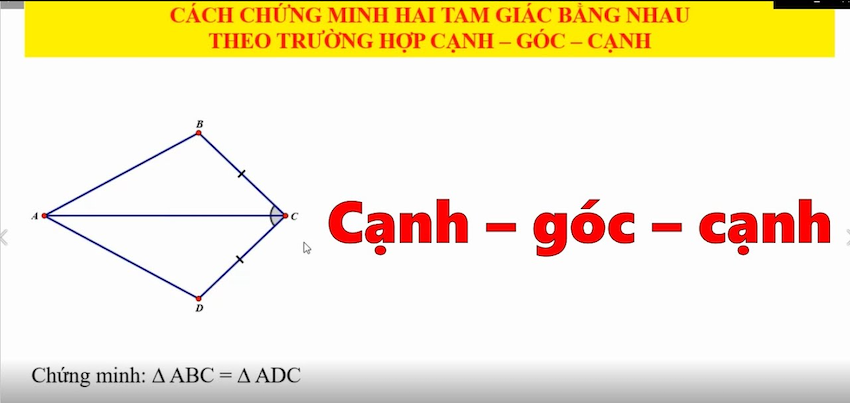
Tiêu chuẩn cạnh – góc – cạnh (SAS)
- Hai cạnh và góc kẹp giữa bằng nhau
- Cách xác định các yếu tố tương ứng
- Quy trình chứng minh
- Bài tập mẫu
Tiêu chuẩn góc – cạnh – góc (ASA)
- Hai góc và cạnh chung bằng nhau
- Trường hợp áp dụng
- Phương pháp chứng minh
- Ví dụ thực hành
Tiêu chuẩn góc – góc – cạnh (AAS)
- Hai góc và cạnh không kẹp giữa bằng nhau
- Điều kiện sử dụng
- Các bước thực hiện
- Bài toán minh họa
Phương pháp chứng minh chi tiết
Các bước cơ bản
- Xác định các yếu tố đã cho
- Chọn tiêu chuẩn phù hợp
- Lập luận chặt chẽ
- Kết luận
Kỹ thuật chứng minh
- Vẽ hình minh họa
- Ghi chú các yếu tố bằng nhau
- Sắp xếp logic các bước
- Kiểm tra lại kết quả
Ứng dụng trong chương trình học tại Canada
Các môn học liên quan
- Hình học Euclidean
- Giải tích hình học
- Toán ứng dụng
- Thiết kế kỹ thuật

Tầm quan trọng trong nghiên cứu
- Phát triển tư duy không gian
- Kỹ năng phân tích
- Khả năng giải quyết vấn đề
- Tư duy logic
Lỗi thường gặp và cách khắc phục
Lỗi phổ biến
- Nhầm lẫn các tiêu chuẩn
- Thiếu sót trong chứng minh
- Kết luận vội vàng
- Bỏ qua điều kiện cần
Cách tránh sai sót
- Đọc kỹ đề bài
- Vẽ hình chính xác
- Kiểm tra từng bước
- Xem xét các trường hợp đặc biệt
Phương pháp học tập hiệu quả
Cách ghi nhớ
- Tạo sơ đồ tư duy
- Thực hành nhiều bài tập
- Liên hệ với thực tế
- Học nhóm tương tác

Tài liệu tham khảo
- Sách giáo khoa Canada
- Tài liệu trực tuyến
- Video hướng dẫn
- Bài tập thực hành
Chuẩn bị cho kỳ thi tại Canada
Kiến thức cần thiết
- Nắm vững các tiêu chuẩn
- Thành thạo các phương pháp chứng minh
- Hiểu rõ ứng dụng thực tế
- Biết cách giải quyết bài tập tổng hợp
Chiến lược làm bài
- Phân tích đề bài
- Vẽ hình minh họa
- Lựa chọn phương pháp
- Trình bày logic
Ví dụ bài tập và lời giải
Bài tập mẫu 1
- Đề bài
- Phân tích
- Các bước giải
- Kết luận

Bài tập mẫu 2
- Tình huống
- Cách tiếp cận
- Giải chi tiết
- Kiểm tra kết quả
Kết luận
Việc nắm vững cách chứng minh hai tam giác bằng nhau là nền tảng quan trọng cho việc học tập toán học tại Canada. Không chỉ giúp bạn đạt điểm cao trong các kỳ thi, kiến thức này còn phát triển tư duy logic và khả năng giải quyết vấn đề – những kỹ năng thiết yếu cho sinh viên quốc tế.
Để được tư vấn thêm về việc chuẩn bị kiến thức cho du học Canada, vui lòng liên hệ:
Thông tin liên hệ:
- Email: [email protected]
- Website: https://canada.net.vn
Đội ngũ tư vấn viên tại canada.net.vn luôn sẵn sàng hỗ trợ bạn trong việc chuẩn bị hành trang kiến thức vững chắc cho hành trình du học Canada.

