Trong chương trình học toán tại các trường đại học Canada, hình học không gian và phẳng đóng vai trò quan trọng, đặc biệt là các bài toán về tam giác đều và đường tròn ngoại tiếp. Bài viết này sẽ hướng dẫn chi tiết cách xác định tâm đường tròn ngoại tiếp tam giác đều, một kiến thức cơ bản nhưng thiết yếu cho sinh viên quốc tế.
Tổng Quan Về Tam Giác Đều Và Đường Tròn Ngoại Tiếp
Định Nghĩa Và Tính Chất Cơ Bản
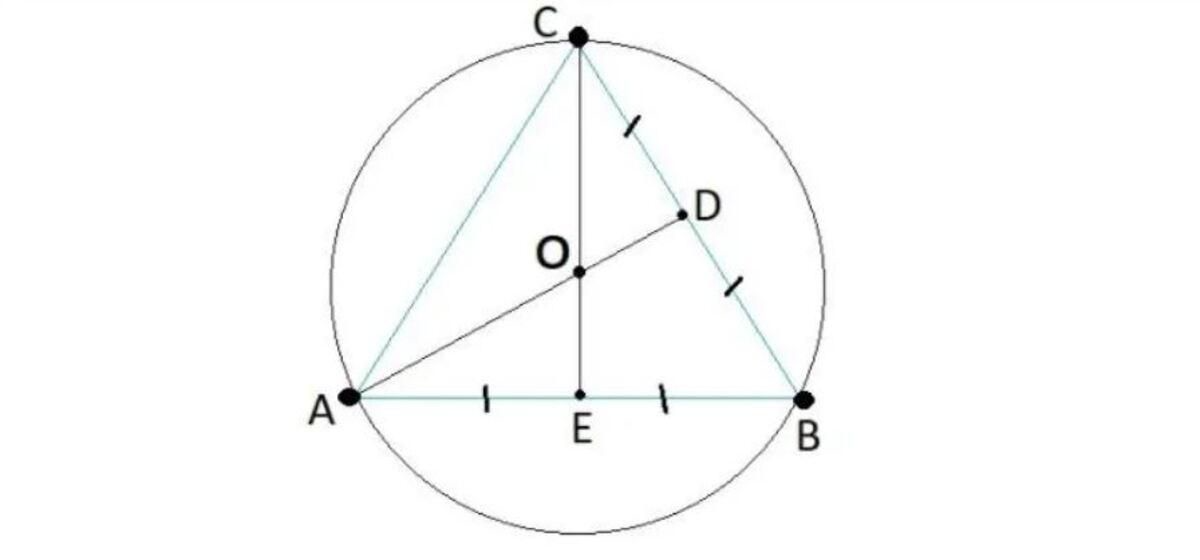
Tam giác đều là tam giác có ba cạnh bằng nhau và ba góc bằng nhau (mỗi góc 60°). Đường tròn ngoại tiếp tam giác là đường tròn đi qua cả ba đỉnh của tam giác. Đối với tam giác đều, tâm đường tròn ngoại tiếp có những đặc điểm độc đáo:
- Là giao điểm của ba đường trung trực
- Cách đều ba đỉnh của tam giác
- Nằm trên đường cao của tam giác
Các Yếu Tố Quan Trọng
Trong tam giác đều ABC:
- Ba cạnh bằng nhau: AB = BC = CA
- Ba góc bằng nhau: ∠A = ∠B = ∠C = 60°
- Ba đường cao bằng nhau
- Ba đường trung tuyến bằng nhau
- Ba đường trung trực bằng nhau
Xem thêm Nguyên Hàm Của Sinx: Hướng Dẫn Chi Tiết Và Ứng Dụng Trong Giáo Dục Canada
Phương Pháp Xác Định Tâm Đường Tròn Ngoại Tiếp
Phương Pháp 1: Sử Dụng Đường Trung Trực
- Bước 1: Vẽ đường trung trực của một cạnh
- Lấy điểm giữa của cạnh
- Vẽ đường vuông góc với cạnh tại điểm giữa
- Bước 2: Vẽ đường trung trực của cạnh thứ hai
- Lặp lại quy trình trên
- Giao điểm của hai đường trung trực chính là tâm đường tròn ngoại tiếp
- Bước 3: Kiểm tra
- Đo khoảng cách từ tâm đến ba đỉnh
- Các khoảng cách này phải bằng nhau

Phương Pháp 2: Sử Dụng Đường Cao
- Bước 1: Vẽ một đường cao
- Vẽ đường vuông góc từ một đỉnh xuống cạnh đối diện
- Bước 2: Xác định điểm
- Tâm đường tròn ngoại tiếp nằm trên đường cao
- Cách đỉnh một khoảng bằng 1/3 đường cao
Các Công Thức Và Tính Toán
Công Thức Cơ Bản
- Bán kính đường tròn ngoại tiếp (R):
- R = a/(√3) Trong đó a là độ dài cạnh tam giác
- Diện tích tam giác (S):
- S = (a²√3)/4
- Khoảng cách từ tâm đến cạnh (r):
- r = a√3/3
Ứng Dụng Trong Tính Toán
- Tính toán diện tích đường tròn ngoại tiếp:
- Sđt = πR²
- Tính chu vi đường tròn ngoại tiếp:
- Cđt = 2πR

Ứng Dụng Trong Giáo Dục Canada
Tầm Quan Trọng Trong Chương Trình Học
Tại các trường đại học Canada như University of Toronto hay McGill University, kiến thức về tam giác đều và đường tròn ngoại tiếp được ứng dụng trong:
- Khóa học Hình học cao cấp
- Thiết kế đồ họa máy tính
- Kiến trúc và xây dựng
- Kỹ thuật cơ khí
Phương Pháp Giảng Dạy
Các trường Canada áp dụng phương pháp giảng dạy hiện đại:
- Sử dụng phần mềm mô phỏng 3D
- Thực hành trên máy tính
- Kết hợp lý thuyết và thực hành
Xem thêm Cách Chứng Minh Hai Tam Giác Bằng Nhau – Kiến Thức Hình Học Cơ Bản Cho Du Học Sinh Canada
Bài Tập Và Ví Dụ
Bài Tập Cơ Bản
- Cho tam giác đều ABC cạnh 6cm. Tính:
- Bán kính đường tròn ngoại tiếp
- Diện tích tam giác
- Khoảng cách từ tâm đến cạnh
- Xác định tọa độ tâm đường tròn ngoại tiếp khi biết tọa độ ba đỉnh

Bài Tập Nâng Cao
- Chứng minh các tính chất:
- Tâm đường tròn ngoại tiếp cách đều ba đỉnh
- Tâm nằm trên đường cao
- Giải quyết các bài toán phức hợp:
- Tính góc giữa đường cao và đường tròn ngoại tiếp
- Xác định vị trí tương đối của các đường tròn ngoại tiếp
Mẹo Học Tập Và Luyện Tập
Chiến Lược Học Hiệu Quả
- Hiểu rõ tính chất cơ bản
- Thực hành vẽ hình thường xuyên
- Sử dụng công cụ hỗ trợ học tập
- Làm nhiều bài tập đa dạng
Công Cụ Hỗ Trợ
- Phần mềm hình học động:
- GeoGebra
- Cabri Geometry
- Maple
- Tài liệu tham khảo online:
- Khan Academy
- Mathematics Stack Exchange

Chuẩn Bị Cho Du Học Canada
Kiến Thức Nền Tảng
- Ôn tập các khái niệm cơ bản
- Làm quen với thuật ngữ tiếng Anh
- Thực hành giải bài tập đa dạng
Tài Liệu Học Tập
- Sách giáo khoa Canada:
- Canadian Mathematics
- Advanced Geometry
- Nguồn tài liệu online:
- Canadian Mathematical Society
- Mathematics Education Resources
Lời Kết
Việc nắm vững cách xác định tâm đường tròn ngoại tiếp tam giác đều không chỉ giúp bạn đạt điểm cao trong các kỳ thi mà còn tạo nền tảng vững chắc cho việc học tập tại Canada. Kiến thức này sẽ được ứng dụng trong nhiều lĩnh vực khác nhau của toán học và các ngành học liên quan.
Để được tư vấn chi tiết về chương trình du học Canada và các khóa học toán, hãy liên hệ với chúng tôi:
Thông tin liên hệ:
- Email: [email protected]
- Website: https://canada.net.vn
Đội ngũ tư vấn của chúng tôi luôn sẵn sàng hỗ trợ bạn trong việc chuẩn bị hành trang kiến thức vững chắc trước khi bắt đầu hành trình du học tại Canada. Hãy để chúng tôi đồng hành cùng bạn trên con đường chinh phục ước mơ du học và phát triển sự nghiệp tại đất nước xinh đẹp này.