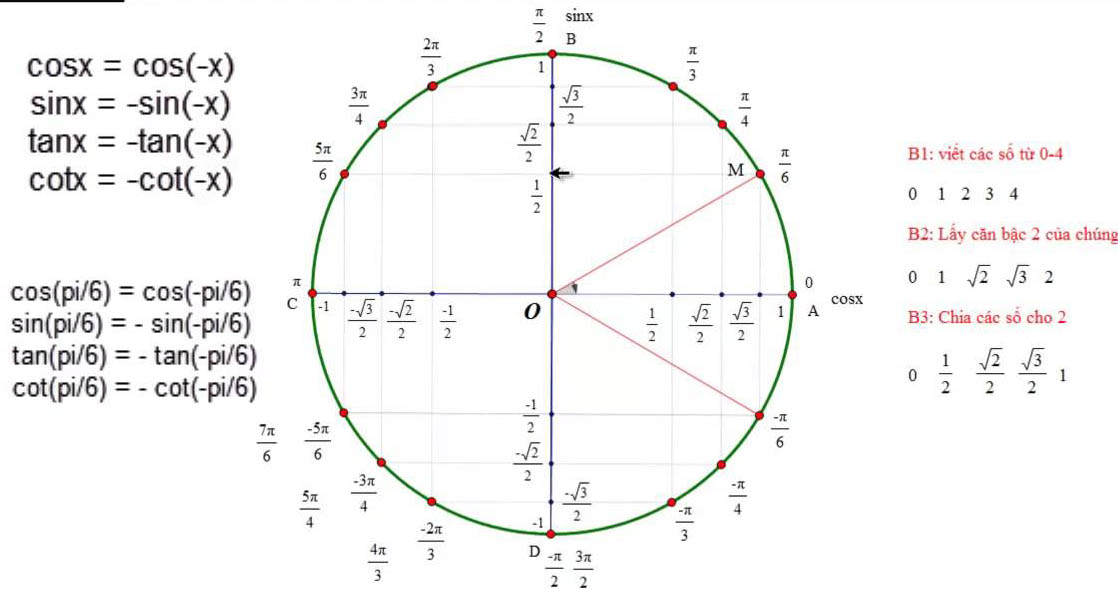
Trong quá trình học tập tại Canada, đặc biệt là đối với các sinh viên theo học các ngành STEM, việc nắm vững kiến thức về lượng giác là vô cùng quan trọng. Hôm nay, canada.net.vn sẽ hướng dẫn chi tiết cách giải phương trình cos x = 1, một dạng bài tập cơ bản nhưng quan trọng trong toán học.
Tại sao cần hiểu rõ phương trình cos x = 1?
Ý nghĩa trong toán học
- Đây là phương trình lượng giác cơ bản
- Thể hiện các điểm đặc biệt trên đường tròn lượng giác
- Là nền tảng cho các bài toán phức tạp hơn
- Ứng dụng trong nhiều lĩnh vực khác nhau
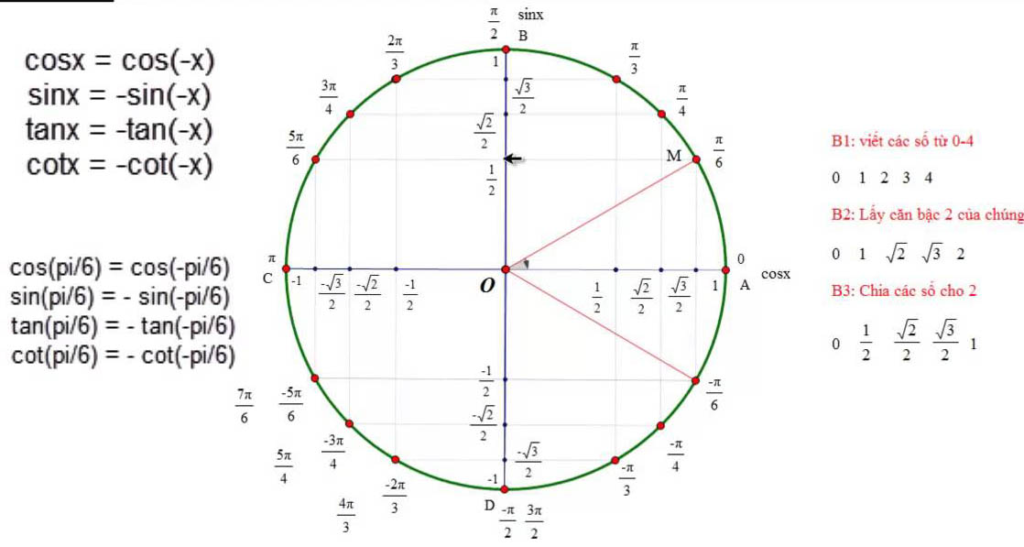
Ứng dụng thực tế tại các trường đại học Canada
- Kỹ thuật điện tử
- Vật lý đại cương
- Cơ học
- Xử lý tín hiệu số
Kiến thức cơ bản cần nắm vững
Đặc điểm của hàm số cos x
- Hàm số tuần hoàn với chu kỳ 2π
- Miền xác định: R (tập số thực)
- Miền giá trị: [-1,1]
- Giá trị đặc biệt tại các góc cơ bản
Các giá trị đặc biệt của cos x
- cos 0° = 1
- cos 90° = 0
- cos 180° = -1
- cos 270° = 0
- cos 360° = 1

Phương pháp giải phương trình cos x = 1
Bước 1: Xác định điểm xuất phát
Khi cos x = 1, điều này có nghĩa là:
- Góc x nằm trên đường tròn lượng giác
- Điểm tương ứng nằm tại (1,0) trên đường tròn đơn vị
Bước 2: Tìm nghiệm tổng quát
Do tính chất tuần hoàn của hàm cos:
- x = 2kπ (với k ∈ Z)
- Trong đó k là số nguyên bất kỳ
Bước 3: Biểu diễn tập nghiệm
Tập nghiệm có thể viết dưới dạng: S = {2kπ | k ∈ Z}
Ví dụ minh họa và ứng dụng
Ví dụ 1: Tìm các nghiệm trong khoảng [0, 4π]
- Thay k = 0: x = 0
- Thay k = 1: x = 2π
- Thay k = 2: x = 4π
Ví dụ 2: Ứng dụng trong vật lý
- Dao động điều hòa
- Sóng âm
- Dòng điện xoay chiều

Phương pháp ghi nhớ và luyện tập
Cách ghi nhớ hiệu quả
- Vẽ đường tròn lượng giác
- Đánh dấu các điểm đặc biệt
- Liên hệ với chu kỳ 2π
- Thực hành nhiều bài tập
Các dạng bài tập thường gặp
- Tìm nghiệm trong khoảng cho trước
- Kết hợp với các bất phương trình
- Ứng dụng trong các bài toán thực tế
Xem thêm Hướng Dẫn Chi Tiết Công Thức Tính Diện Tích Toàn Phần Cho Du Học Sinh Canada
Ứng dụng trong chương trình học tại Canada
Các môn học liên quan
- Giải tích (Calculus)
- Vật lý đại cương
- Kỹ thuật điện
- Xử lý tín hiệu
Tầm quan trọng trong nghiên cứu
- Phân tích dao động
- Xử lý tín hiệu số
- Thiết kế mạch điện
- Mô phỏng vật lý

Lỗi thường gặp và cách khắc phục
Lỗi phổ biến
- Quên tính chất tuần hoàn
- Nhầm lẫn với các giá trị đặc biệt
- Sai sót trong chuyển đổi đơn vị
- Bỏ sót nghiệm
Cách tránh sai sót
- Kiểm tra lại các bước giải
- Vẽ đồ thị minh họa
- Thực hành nhiều dạng bài
- Hiểu rõ ý nghĩa hình học
Xem thêm Hướng Dẫn Chi Tiết về Đạo Hàm Logarit Tự Nhiên (ln) Cho Du Học Sinh Canada
Tài nguyên học tập bổ sung
Sách và tài liệu tham khảo
- Sách giáo khoa Canada
- Tài liệu luyện thi
- Bài tập và đề thi mẫu
- Video hướng dẫn
Công cụ học tập online
- Phần mềm GeoGebra
- Các website toán học
- Ứng dụng di động
- Forums học tập

Chuẩn bị cho kỳ thi tại Canada
Kỹ năng cần thiết
- Nắm vững lý thuyết
- Thành thạo các công thức
- Kỹ năng giải nhanh
- Khả năng kiểm tra kết quả
Chiến lược làm bài
- Đọc kỹ đề bài
- Vẽ hình minh họa
- Giải theo các bước
- Kiểm tra lại kết quả
Kết luận
Việc nắm vững cách giải phương trình cos x = 1 không chỉ giúp bạn đạt điểm cao trong các kỳ thi mà còn tạo nền tảng vững chắc cho việc học tập các môn học khác tại Canada. Hãy chăm chỉ luyện tập và áp dụng các phương pháp học tập hiệu quả để đạt được kết quả tốt nhất.
Để được tư vấn thêm về du học Canada và các khóa học toán học, vui lòng liên hệ:
Thông tin liên hệ:
- Email: [email protected]
- Website: https://canada.net.vn
Đội ngũ tư vấn viên tại canada.net.vn luôn sẵn sàng hỗ trợ bạn trong việc chuẩn bị kiến thức và kỹ năng cần thiết cho hành trình du học Canada.